Sedekah Ilmu: Turunan Fungsi dan Tururan Fungsi Trigonometri

Turunan Fungsi dan Tururan Fungsi Trigonometri

Pengertian Turunan Fungsi

Turunan Fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalkan fungsi f menjadi f’ yang memiliki nilai tidak beraturan.

Aturan-aturan dalam turunan fungsi ialah:

f(x), menjadi f'(x) = 0

Apabila f(x) = x, maka f’(x) = 1

Aturan pangkat : apabila f(x) = xn, maka f’(x) = n X n – 1

Aturan kelipatan konstanta : apabila (kf) (x) = k. f’(x)

Aturan rantai : apabila ( f o g ) (x) = f’ (g (x)). g’(x))

Rumus-Rumus Turunan Fungsi Al Jabar

Rumus Turunan Fungsi Pangkat

Turunan Fungsi berbentuk pangkat, turunannya dapat menggunakan rumus sebagai berikut:

$f'(x) = \lim \limits_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$f'(x) = \lim \limits_{h \to 0}\frac{(x+h)^n - (x)^n}{h}$

$= \lim \limits_{h \to 0}\frac{\sum^n_{i=0}C^n_ix^{n-i}h^i-x^n}{h}$

$= \lim_{h \to 0}\frac{C^n_0x^n+C^n_1x^{n-1}h+C^n_2x^{n-2}h^2+\cdots+C^n_nh^n-x^n}{h}$

$= \lim \limits_{h\to0}\frac{x^n+nx^{n-1}h+\frac{n(n-1)}{2!}x^{n-2}h^2+\cdots+h^n-x^n}{h}$

$= \lim \limits_{h\to0}\frac{nx^{n-1}h+\frac{n(n-1)}{2!}x^{n-2}h^2+\cdots+h^n}{h}$

$= \lim \limits_{h\to0}(nx^{n-1}+\frac{n(n-1)}{2!}x^{n-2}h+\cdots+h^{n-1})$

$= nx^{n-1}+0+0+\cdots+0=nx^{n-1}$

Maka, rumus turunan fungsi pangkat ialah:

$f'(x ) = nx^{n-1}$

2. Rumus turunan hasil kali fungsi 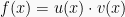$f(x) = u(x) \cdot v(x)$

Rumusan Fungsi f(x) turunan yang terbentuk dari perkalian fungsi u(x) dan v(x), adalah:

$f'(x) = \lim \limits_{h\to0}\frac{f(x+h)-f(x)}{h}$

$\lim \limits_{h\to0}=\frac{u(x+h)v(x+h)-u(x)v(x)}{h}$

$\lim \limits_{h\to0}=\frac{u(x+h)v(x+h)-u(x+h)v(x)+u(x+h)v(x)-u(x)v(x)}{h}$

$=\lim\limits_{h\to0}\frac{[u(x+h)v(x+h)-u(x+h)v(x)]+[u(x+h)v(x)-u(x)v(x)]}{h}$

$= \lim \limits_{h\to0}\frac{u(x+h)[v(x+h)-v(x)]}{h}+\lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)}{h}$

$= \lim \limits_{h\to0}u(x+h) \cdot \lim \limits_{h\to0}\frac{v(x+h)-v(x)}{h}+\lim \limits_{h\to0}\frac{u(x+h)-u(x)}{h}.\lim_{h\to0}v(x)$

$= u(x+0) \cdot v'(x)+u'(x) \cdot v(x)$

$u'(x).v(x)+u(x).v'(x)\overset{atau}{\rightarrow}u'.v+u.v'$

Maka, rumus turunan fungsinya ialah:

$f'(x)=u'v+uv'$

3. Rumus turunan fungsi pembagian $f(x)=\frac{u(x)}{v(x)}$

Rumus turunan fungsi pembagian dapat di tentukan dengan menggunakan rumus:

$f'(x) = \lim \limits_{h\to0}\frac{f(x+h)-f(x)}{h}\overset{menjadi}{\rightarrow}\lim \limits_{h\to0}\frac{\frac{u(x+h)}{v(x+h)} - \frac{u(x)}{v(x)}}{h}$

Sehingga,

$f'(x) = \lim \limits_{h\to0}\frac{u(x+h)v(x)-u(x)v(x+h)}{h \cdot v(x+h)v(x)}$

$=\lim \limits_{h\to0}\frac{u(x+h)v(x)-u(x)v(x)-u(x)v(x+h)+u(x)v(x)}{h.v(x+h)v(x)}$

$= \lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)-u(x)[v(x+h)-v(x)]}{h.v(x+h)v(x)}$

$= \lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)}{h \cdot v(x+h)v(x)} - \lim \limits_{h\to0}\frac{u(x)[v(x+h)-v(x)]}{h \cdot v(x+h)v(x)}$

$=\lim \limits_{h\to0}\frac{u(x+h)-u(x)}{h}.\lim\limits_{h\to0}\frac{v(x)}{v(x+h)v(x)}- \lim\limits_{h\to0}\frac{u(x)}{v(x+h)v(x)}.\lim\limits_{h\to0}\frac{v(x+h)-v(x)}{h}$

$= u'(x).\frac{v(x)}{v(x+0)v(x)}-\frac{u(x)}{v(x+0)v(x)} \cdot v'(x)$

$=\frac{u'(x)v(x)}{v(x)v(x)}-\frac{u(x)v'(x)}{v(x)v(x)} \rightarrow\frac{u'(x)v(x)-u(x)v'(x)}{(u(x))^2} \rightarrow \frac{u'v-uv'}{v^2}$

Maka, rumus turunan fungsinya adalah

$f'(x) = \frac{u'v-uv'}{v^2}$

4. Rumus turunan pangkat dari fungsi 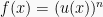$f(x)=(u(x))^n$

Perlu diingat, apabila $f(x) = x^n$ , maka:

$f'(x)=\frac{df(x)}{dx}= \frac{dx^n}{dx} = nx^n-1$

Karna $f(x) = (u(x))^n=u^n$ , maka:

$f'(x) = \frac{df(x)}{dx} = \frac{du^n}{dx} \cdot \frac{du}{du}$

Atau,

$f'(x) = \frac{du^n}{du} \cdot \frac{du}{dx} = nu^{n-1} \cdot u'$

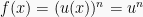Maka, rumus turunan fungsinya ialah:

$f'(x) = nu^(n-1) \cdot u'$

4. Rumus-rumus Turunan Trigonometri

Berdasarkan definisi turunan, maka dapat diperoleh rumus-rumus turunan trigonometri yakni sebagai berikut: (dengan u dan v masing-masing fungsi dari x), yakni:

$y = \sin x \rightarrow y' = \cos x$

$y = \cos x \rightarrow y' = - \sin x$

$y = \tan x \rightarrow y' = \sec^2 x$

$y = \cot x \rightarrow y' = - \csc^2 x$

$y = \sec x \rightarrow y'$

$y = \csc x \rightarrow - \csc \times \cot x$

$y = \sin^n x y' = n \sin^{n-1} \times \cos x$

$y = \cos^nx \rightarrow y' = -n \cos^{n-1} \times \sin x$

$y = \sin u \rightarrow y' = u' \cos u$

$y = \cos u \rightarrow y' = - u' \sin u$

$y = \tan u \rightarrow y' = u' \sec^2 u$

$y = \cot u \rightarrow y' =-u' \csc^2u$

$y = \sec u \rightarrow y' = u' \sec u \tan u$

$y = \csc u \rightarrow y' = -u' \csc u \cot u$

$y = \sin^nu \rightarrow y' = n.u' \sin^{n-1} \cos u$

$y = \cos ^nu \rightarrow y'= -n \cdot u' cos^{n-1}u \cdot \sin u$

Contoh Soal dan Pembahasannya

Contoh soal 1:

Tentukanlah turunan fungsi dari f(x) = 2x(x4 – 5).

Pembahasan:

Misalkan apabila u(x) = 2x dan v(x) = x4 – 5, maka:

u‘ (x) = 2 dan v‘ (x) maka = 4x3

Dengan demikian, diperoleh penjabaran dan hasilnya:

f ‘(x) = u ‘(x).v(x) + u(x).v ’(x) = 2(x4 – 5) + 2x(4x3 ) = 2x4 – 10 + 8x4 = 10x4 – 10

Pengertian Turunan Fungsi Trigonometri

Turunan Fungsi Trigonometri adalah turunan yang fungsi sinus dan kosinus, yang di dapat dari konsep limit atau persamaan turunan yang melibatkan fungsi – fungsi trigonometri seperti sin, cos, tan, cot, sec dan csc.

Jika y=sin x maka y’ = cos x

Jika y=cos x maka y’ = –sin x

Dari rumus dasar diatas tersebut, diturunkanlah rumus pengembangan, yaitu turunan fungsi tangens, cotangens, secan dan cosecan. Proses pengembangan rumus tersebut ialah ;

y = tan x maka y’ = sec2x
y = cot x maka y’ = – cosec2x
y = sec x maka y’ = sec x . tan x
y = cosec x maka y’ = – cosec x . tan x

Maka, terdapat rumus pengembangan turunan fungsi trigonometri dengan aturan rantai, yaitu sebagai berikut ini ;
Misalkan u(x) merupakan fungsi yang terdefinisi pada x bilangan real dan f(u) = sin u, maka untuk y= f [u(x)] diperoleh y’ = f ‘ [u(x)]. u’(x)
y’= (cos u)(u’)

y’= u’.cos u

Rumus Turunan Fungsi Trigonometri

Berikut ini ialah beberapa turunan dasar trigonometri yang harus diketahui sebelum anda memecahkan persoalan turunan trigonometri ;

Jika f(x)= sin x → f ‘(x) = cos x

Jika f(x)= cos x → f ‘(x) = −sin x

Jika f(x)= tan x → f ‘(x) = sec2 x

Jika f(x)= cot x → f ‘(x) = −csc2x

Jika f(x)= sec x → f ‘(x) = sec x . tan x

Jika f(x)= csc x → f ‘(x) = −csc x . cot x.

Contoh Soal